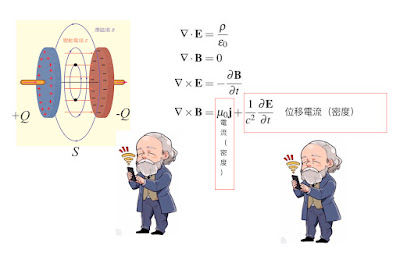
位移電流與馬克士威方程式
當電流 I 流過圖示的平行電板,電流無法直接流過平行電板中間的區域 S,而是正、負電荷 分別同步累積在左、右兩邊的平行電板上,因此電流雖然沒有「直接」流過 S 區域,但是左方導線的電流卻不會受到平行電板的阻礙,依然遵守電荷守恆定律、順暢的流動,好像有一種「等效電流」直接穿過 S 區域。
馬克士威認為平行電板中間的空間 S 區域 ,雖然沒有「真正的電流」流動,但是平行電板電荷累積的過程,S 區域(和所有空間)的電場 E 會隨時間改變,因此 S 區域變動的電場應該可以視同「等效電流」。最後他把右圖所示的安培定律,原本只有電流 I 貢獻的方程式右手邊,加上一項電場 E 隨時間變化的影響,同時把等效電流命名為「位移電流」。
因為方程式每一項的單位都相同,馬克士威為了把加上去的電場變化視同電流,必須在位移電流項加上適當的單位,結果發現光速 c 會自然的出現在這個方程式。
因此馬克士威加上去的位移電流,不但讓「電流」順暢的流過 S 區域 ,同時也完整的整合所有電磁學方程式,是電磁學研究的重大突破。意外發現電磁場和光速有關,更讓馬克士威推論光波就是電磁波的一種,最後也被實驗證實。